Category: Հանրահաշիվ

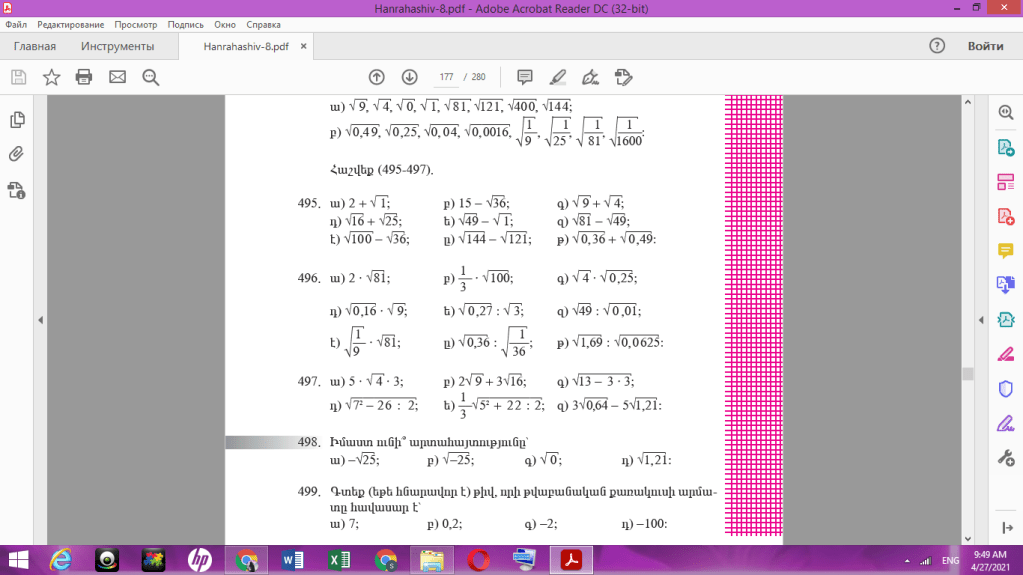
496.

Ա․ 2 . √81=2 . 9=18

Բ․ 1/3 . √100=1/3 . 10=10/3

Գ․ √4 . √0,25=2 . 0,5=1

Դ․ √0,16 . √9=0,4 . 3=1,2

Ե․ √27:3=9=3

Զ․ √49:0,01=4900=70

Ը․ √0,36 : √1/36=0,6 : 1/6

497.

Ա․ 5 . √4 . 3=5 . 2 . 3=30

Բ․ 2√9+3√16=2 . 3 + 3 . 4=18

Գ․ √13 – 3 . 3=13-9=4=2

 √9=3

 √4=2

 √0=0

 √ √1=1

 √81=9

 √121=11

 √400=20

 √144

 √0,49=0,7

 √0,25=0,5

 √0,04=0,2

 √0,0016=0,004

 √1/9=1/3

 √1/25=1/5

 √1/81=1/9

 √1/1600=1/40

495

ա) (3; +∞)

բ) (1; +∞)

գ) (4; +∞)

դ) (-3; +∞)

ա) (2; 7)

բ) (-1; 3)

գ) (-5; 0)

դ) (-16; -10)

ա) ∅

բ) (-7; -5)

գ) ∅

դ) (-5; 0)

445

448

450

1.Հետազոտիր ուղղի և շրջանագծի փոխադարձ դասավորությունը՝ համեմատելով շրջանագծի շառավիղը և կենտրոնից մինչև ուղիղը եղած հեռավորությունը:
Ձևակերպեք ստացված արդյունքները:

2.Ցույց տուր մի կետից շրջանագծին տարված շոշափողի հատվածները հավասար են, և դրանք կազմում են հավասար անկյուններ այն ուղղի հետ, որն անցնում է այդ կետով ու շրջանածի կենտրոնով:

3. Գրիր երկու ճշմարիտ անհավասարության օրինակներ:

34 < 179

94 > 73

Բերված  ճշմարիտ անհավասարություններով  ստացիր  նոր ճշմարիտ անհավասարությունները.

ա/երկու մասը բազմապատկելով միևնույն դրական թվով

340 < 1790

940 > 730

բ/ երկու մասը բազմապատկելով միևնույն բացասական  թվով

-340 > -1790

-940 < -730

գ/յուրաքանչյուր թիվ փոխարինիր իր հակադիրով

-34 > -179

-94 < -73

դ/յուրաքանչյուր թիվ փոխարինիր իր հակադարձով:

1/34 > 1/179

1/94 < 1/73

4. Բեր մեկ անհայտով առաջին աստիճանի անհավասարման օրինակներ 

/ չորս հատ/:

x + 7 > 5

x + 4 > 2

x + 10 > 15

x + 3 > 19

Լուծիր բերված անհավասարման օրինակները, պատկերիր լուծումը թվային ուղղի վրա, նշիր լուծումը միջակայքով:

x + 7 > 5, x > 7 — 5, x > 2 (2;+∞)

x + 4 > 2, x > 4 — 2, x > 2 (2;+∞)

x + 10 > 15, x > 15 — 10, x > 5 (5;+∞)

x + 3 > 19, x > 19 — 3, x > 16 (16;+∞)